Q1 常用的损失函数有哪些
(1) 0-1 loss
记录分类错误的次数。
(2)Hinge Loss
最常用在SVM中最大优化间隔分类中,对可能的输出t=±1和分类器分数y,预测值y的hinge loss定义如下:
L(y)=max(0.1-t*y)
(3)Log Loss对数损失
对于对数函数,由于其具有单调性,在求最优化问题时,结果与原始目标一致,在含有乘积的目标函数中(如极大似然函数),通过取对数可以转化为求和的形式,从而大大简化目标函数的求解过程。
(4)Squared Loss 平方损失
即真实值与预测值之差的平方和。通常用于线性模型中,如线性回归模型。
(5)Exponential Loss指数损失
指数函数的特点是越接近正确结果误差越小,Adaboost算法即使用的指数损失目标函数。但是指数损失存在的一个问题是误分类样本的权重会指数上升,如果数据样本是异常点,会极大地干扰后面基本分类器学习效果。
Q2 如何判断函数凸或非凸
首先定义凸集,如果x,y属于某个集合M,并且所有的θx+(1-θ)f(y)也属于M,那么M为一个凸集。如果函数f的定义域是凸集,并且满足
则该函数为凸函数。
如果函数存在二阶导并且为正,或者多元函数的Hessian矩阵半正定则均为凸函数。
Q3 什么是数据不平衡问题,应该如何解决
数据不平衡又称样本比例失衡,比如二分类问题,如果标签为1的样本占总数的99%,标签为0的样本占比1%则会导致判断失误严重,准确率虚高。
常见的解决不平衡问题的方法如下。
数据采样
数据采样分为上采样和下采样,上采样是将少量的数据通过重复复制使得各类别比例均衡,不过很容易导致过拟合问题,所以需要在新生成的数据中加入随机扰动。
下采样则相反,下采样是从多数类别中筛选出一部分从而使得各类别数据比例维持在正常水平,但容易丢失比较重要的信息,所以应该多次随机下采样。
数据合成是利用已有样本的特征相似性生成更多的样本。
加权是通过不同类别的错误施加不同的权重惩罚,使得ML时更侧重样本较少并容易出错的样本。
一分类
当正负样本比例失衡时候,可以利用One-class SVM,该算法利用高斯核函数将样本空间映射到核空间,在核空间找到一个包含所有数据的高维球体。如果测试数据位于这个高维球体之中,则归为多数类,否则为少数类。
Q4 熵、联合熵、条件熵、KL散度、互信息定义
熵在物理中是用于衡量一个热力学系统的无序程度,表达式为△S=Q/T,其中Q是吸收或者释放的热量,T是温度。
计算机领域将其定义为离散随机事件出现的概率。一个系统越是有序信息熵就会越低;反之,系统越是混乱,信息熵就越高。
联合熵:两个随机变量X,Y的联合分布可求得联合熵。
条件熵:在随机变量X发生的前提下,随机变量Y带来的新的熵,即为Y的条件熵。
其含义是衡量在已知随机变量X的条件下随机变量Y带来的新的熵即为Y的条件熵。
KL散度:两个概率分布(probability distribution)间差异的非对称性度量。
互信息:两个随机变量X,Y的互信息定义为X,Y的联合分布和各自独立分布乘积的KL散度。
Q5 主成分分析和因子分析的区别
在数据挖掘时,变量之间信息的高度重叠和高度相关会给结果分析带来很多障碍。所以需要在削减变量的个数的同时尽可能保证信息丢失和信息不完整。
主成分分析:将一组有一定相关性的指标重新组合成一组个数较少的互不相关的综合新指标,新指标应该既能最大程度反映原变量所代表的信息。又能保证新指标之间保持相互无关。
因子分析:根据相关性大小把原始变量分组,使得组内的变量之间相关性较高,而不同组的变量间的相关性则较低。原始变量进行分解后会得到公共因子和特殊因子。
公共因子是原始变量中共同具有的特征,而特殊因子则是原始变量所特有的部分。
区别:
主成分分析是从空间生成的角度寻找能解释诸多变量变异绝大部分的几组彼此不相关的主成分。而因子分析是寻找对变量起解释作用的公共因子和特殊因子,以及公共因子和特殊因子组合系数。
因子分析把变量表示成各个因子的线性组合,而主成分分析中则把主成分表示成了各变量的线性组合。
主成分分析中不需要假设,因子分析有一些假设,列如公共因子和特殊因子之间不相关等。
主成分分析中,由于给定的协方差矩阵或者相关矩阵的特殊值是唯一的,所以主成分一般是固定的,而因子分析可以通过旋转得到不同的因子。
Q6 什么是最小风险贝叶斯决策
贝叶斯定理会根据一件事发生的先验知识计算出他的后验概率。数学上,他表示为一个条件样本发生的真正率占真正率和假正率之和的比例:
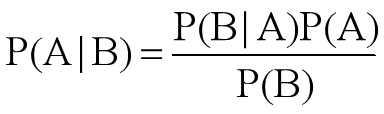
最小贝叶斯决策的算法步骤描述如下:
对于一个实际问题,对于样本xx,最小风险贝叶斯决策的计算步骤如下:
(1)利用贝叶斯公式计算后验概率:
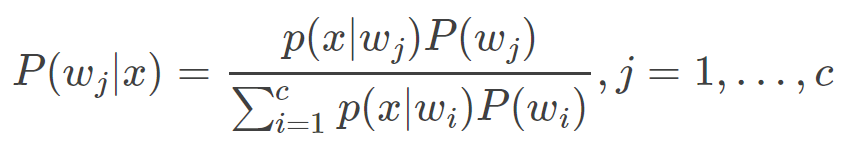
其中要求先验概率和类条件概率已知。
(2)利用决策表,计算条件风险:
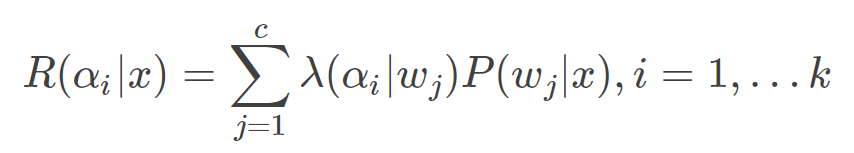
(3)决策:选择风险最小的决策,即:
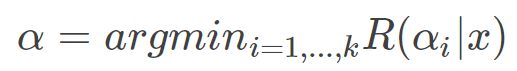
Q7 什么是贝叶斯最小错误概率和最小风险
为了理解贝叶斯,用判别细胞是否为癌细胞为例。状态1为正常细胞,状态2为癌细胞,假设: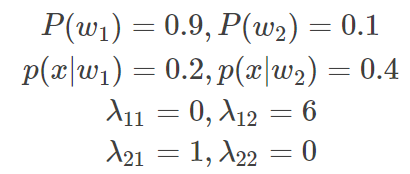
计算得后验概率为: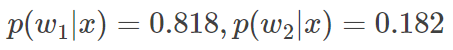
计算条件风险: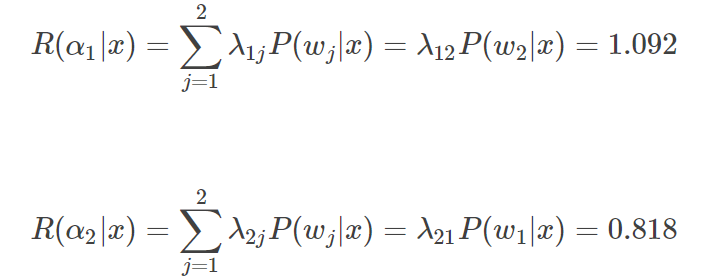
由于R(α1|x)>R(α2|x),即判别为1类的风险更大,根据最小风险决策,应将其判别为2类,即癌细胞。
由此可见,因为对两类错误带来的风险的认识不同,从而产生了与之前不同的决策。显然,但对不同类判决的错误风险一致时,最小风险贝叶斯决策就转化成最小错误率贝叶斯决策。最小错误贝叶斯决策可以看成是最小风险贝叶斯决策的一个特例。

- 本文链接:https://www.tjzzz.com/posts/31aafeb2.html
- 版权声明:本博客所有文章除特别声明外,均默认采用 许可协议。


